一、线性 = 齐次性 + 叠加性

一言以蔽之，满足齐次性和叠加性的映射就是线性的。

什么齐次？用数学的语言表达就是对数乘满足：

这里  是个标量， 是变量，是一个映射。如果觉得「齐次」这个名字不够直观，你可以把它理解为「等比例缩放」。

什么是叠加？就是对加法保持：

有时候会把这两个性质写成一个公式：

也就是说，如果我们能把一个系统的行为用线性映射来描述，那么系统的输入叠加后的输出就等于各自输出的叠加；输入乘以某个系数，输出就乘以同样的系数。

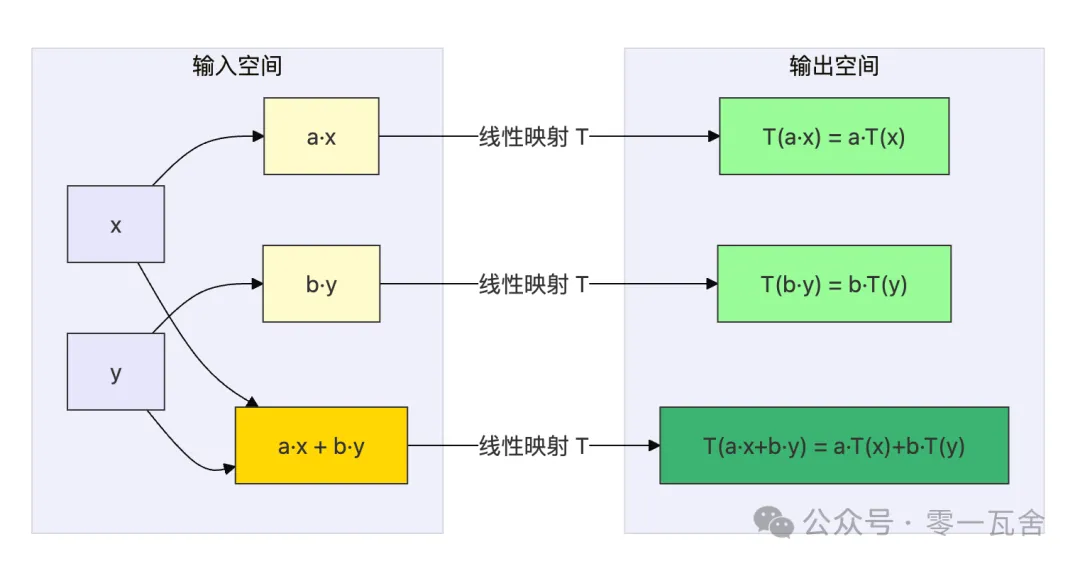
你可以想象一台特殊的复印机：如果你把一张图片放大一倍，然后复印，那么复印出来的图片也会放大一倍。无论你先放大再复印，还是先复印再放大，结果都一样；如果你把两张图片拼在一起复印，那么复印出来的图片就是这两张图片分别复印后的拼接。无论你先把两张图拼起来再复印，还是先分别复印再拼起来，结果都一样。

在现实中，这样的系统非常常见，而且它们在数学上也容易被分析、被分解和被求解，也因此被研究的最普遍。

其实线性已经解释完了。为了论述更系统，我们多说一点。

二、矩阵：线性映射的坐标化

要理解矩阵和矩阵乘法，首先得理解向量空间（Vector Space）的概念。一个向量空间，通俗讲，就是可以「加」并可对其进行数乘（标量乘法）的一个集合。教科书上为了严谨会介绍八个公理，我们这里就省略了，先抓住这两个主要特征即可。最常见的例子是普通的二维空间（）或三维空间（）。再广义一点，函数空间、图像空间等也都可以视为向量空间。

当我们给定一个线性映射 ，如果  和  都是有限维向量空间，那么通过选择各自的基（basis），就能把这个「抽象的」映射用一个矩阵来表达：

具体地说，令  是  的一组基， 是  的一组基。如果一个向量  用坐标表示为

则

由于  是线性的，所以

再将  用  的坐标来表示，我们就能写出「变换后向量的坐标」与「原向量坐标」之间的线性关系。这样，最终得到一个  矩阵 A 使得

这就是从线性映射到矩阵的过程。

三、矩阵乘法：复合线性映射的坐标化

如果手头有两个线性映射  和 ，比如 ，，那将其复合在一起  得到的就是 ，一个从  到  的新线性映射。

现若我们想用坐标来「记录」这些映射，就对应了三个矩阵——分别表示  以及它们的复合映射。如果  被矩阵 （大小 ）表示， 被矩阵 （大小 ）表示，那么它们的复合  就应该由一个  的矩阵  来表示。

要求满足：

所以

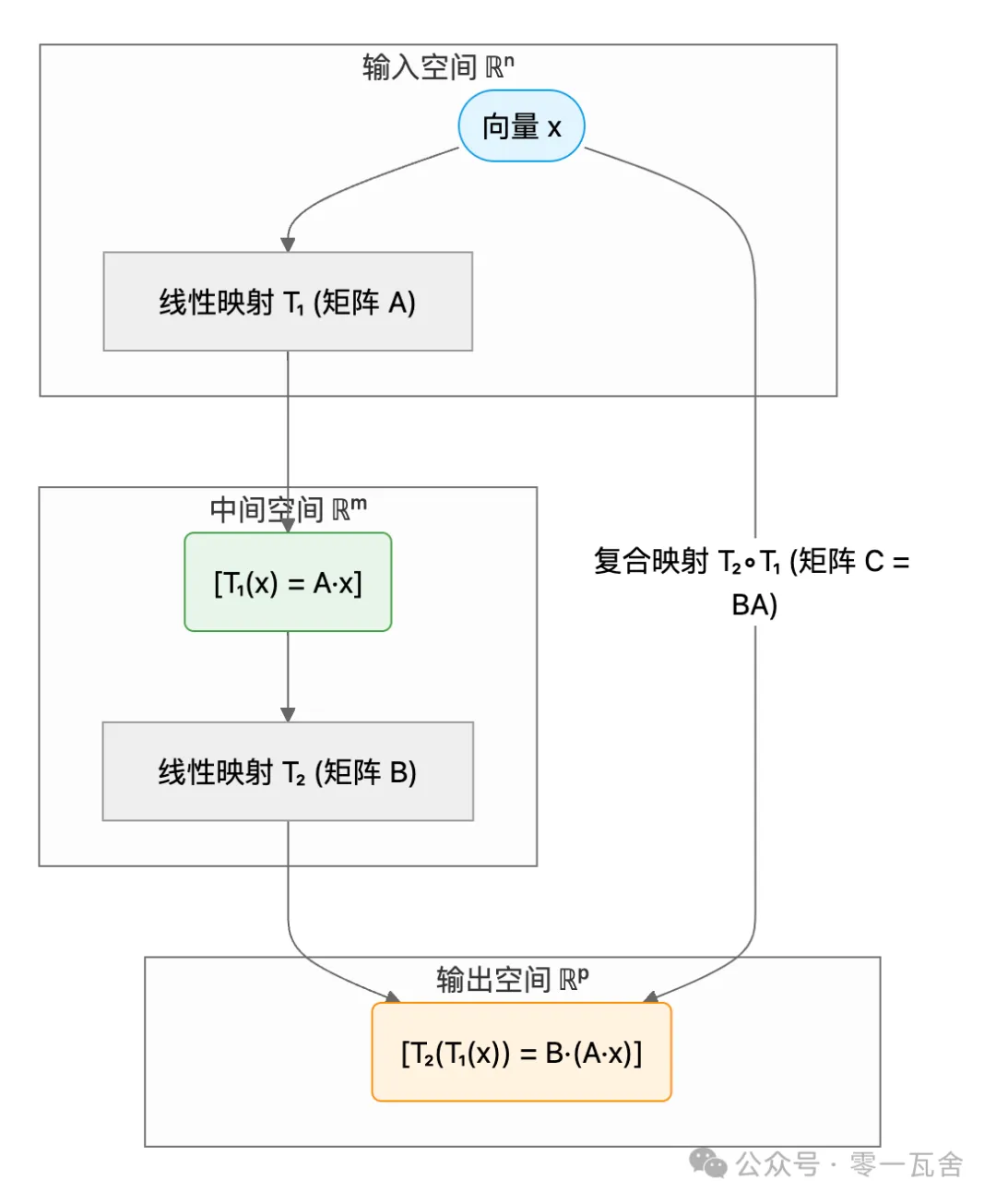
也就是说，矩阵乘法是函数复合在坐标表示下的结果。它保证「先做一个映射，再做另一个映射」在坐标层面是通过矩阵的乘积来表达。其元素计算方式（行乘列求和）虽然第一眼看起来很「怪异」，却恰恰完美地捕捉了「函数复合在坐标表达下的累加原理」。

四、更多视角下的线性代数

4.1 几何视角：从坐标到形变

线性代数经常被介绍为「矩阵方程的求解」，但它实际上贯穿了极其丰富的几何内容。一个  维向量就对应于一个  维空间中的点，线性变换就相当于「把空间做各种均匀的拉伸、旋转、剪切等等」。在三维空间中，我们能直观地看见矩阵对一个立方体的变换：可能扭曲成长方体、平行六面体乃至退化成平面或线。

再往深层看，分析一个线性变换最重要的思路之一是找它的「特征向量」（eigenvector）和「特征值」（eigenvalue）。也就是说，

此时向量  在变换下方向不变，只是「伸缩」了  倍。能找到这些特征向量并分解整个空间，就能极大地简化我们的研究。这也体现了线性变换在几何上对空间的分解：把真正复杂的变化拆成几个「最简单」的生长或衰减模式。

初等线性代数课程里有「对角化」的概念——如果一个矩阵有足够多的特征向量，那么就能在合适的基下把它对角化成最简单的形式。不过，在更抽象的层面，还存在 Jordan 标准形、极分解（Polar Decomposition）、SVD（奇异值分解）……这些工具都是在探究：给定一个线性映射（用矩阵 A 表示），其究竟是什么样的「几何形变」，有着哪些内在不变性或分解结构？

所有这些「抽象研究」都指向同一个事实：线性变换具备可分解、可分析的优良性质。

4.2 高维视角：泛函分析

在线性代数中，我们大多只考虑有限维空间。然而，现实中的波动方程解空间、量子力学态空间、偏微分方程解空间等往往是无限维的。此时我们进入了一个更大的舞台：泛函分析（Functional Analysis）。

• 当向量空间变成「函数空间」或「序列空间」，我们这些熟悉的概念——如向量、线性映射、矩阵乘法——就要换成更一般的算子（operator）和无穷维度的基来重新审视。
• 不过，无论是有限维还是无限维，「线性」与「叠加可复合」这两个关键点是不变的，依然为我们带来类似的分析和分解工具（例如谱定理、紧算子理论、自伴算子研究等）。

从这个角度来说，线性代数的思想远远超越了初等情境，进而渗透到更高层次的数学与物理结构中。

4.3 抽象代数视角：从环到代数、从代数到范畴

如果我们再登高一层，不仅仅把线性代数看作对向量和矩阵的处理，而是站在抽象代数或范畴论的高度，就能看到更丰富的结构：

• 矩阵加法与乘法使得矩阵构成了一个环，甚至是一个代数。
• 线性映射之间的复合在所有向量空间上形成了一个范畴（objects 是向量空间，morphisms 是线性映射）。
• 在范畴论的语言下，我们可以研究极限、上同调、张量积、导出函子等更加高级的概念，而向量空间这个范畴便是其中一个最「体面」、最易操控的例子。

虽然这些话题对初学者而言也许过于抽象，但它们都根植于最简单的「线性组合」与「复合」的概念。换言之，线性代数是更高数学世界里的一块基石。

五、线性系统的普适性

任何一个系统，只要它的核心过程可以被描述为线性映射的连续施加或叠加，那么就会使用矩阵乘法来刻画实际过程或计算结果。当我们在工程、物理或计算机程序中一次次地「使用」矩阵乘法，往往就是在对某个模型做「线性变换的复合操作」。

现实生活中很多系统（如流体的湍流、经济系统、生态系统）似乎并不符合「线性」模型，但但在局部特征、微观近似或扰动分析时，大量的方法还是要借助「线性化」。

• 例如在偏微分方程解的数值方法中，经常要在线性算子上反复迭代或做局部线性逼近。
• 在机器学习的反向传播（backpropagation）中，每一层的更新其实是对参数的局部线性更新（再加上非线性激活函数）。
• 在系统动力学中，Jacobians 矩阵帮助我们理解平衡点的稳定性，也是一种对非线性系统局部行为「线性化」。

在多数情况下，任何复杂系统，若只研究「小范围」或「微扰」下的变化，就可以用泰勒展开等方法做线性近似。也就是说，非线性系统往往可以在一个小区间被「线性化」，而我们关心的第一阶逼近常常够用。

由此可见，就算在研究非线性现象的过程中，线性代数提供的工具仍然不可或缺。

六、再次总结线性系统的特性

• 可分解性：线性运算的最大特色之一是能够「分而治之」——一个向量可以拆成若干基向量的线性组合，映射可以分块作用，然后再把结果加起来。矩阵的行与列正是对「把输入分块，对每块进行加权处理，再将输出组合」的坐标化实现。
• 可复合性：在函数层面，「先做  再做 」对应的是复合 。在线性代数的世界中，这个复合操作变成了「矩阵相乘」，从而使我们能以坐标代数的方法去处理诸多连续或分步的线性操作。
• 可叠加性：世界上大量的自然、物理和工程系统可以（或至少在局部）用线性模型表示，因为它们（暂时）满足叠加原理。在这个意义下，矩阵乘法成为了描述这些「叠加演化」最顺手的工具。
• 不变性：矩阵乘法之下的一系列不变量（迹、行列式、特征值谱……）往往对应某些深层对称或守恒定律；物理学中会关心质量、能量、动量的守恒；在数学中会关心度量、对称性、正交性的保持。